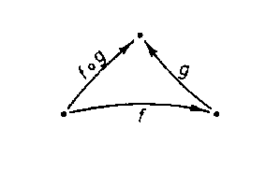
Fig. 1.16.
|
|
- i funksioneve f, g përkufizohet me barazinë :
(  x  A) (  z C) (g  f) :x→z  g (f (x)). (...39)
- Siç shihet në shumëzimin g f renditja e të shkruarit dhe zbatimit të funksioneve f, g ka rëndësi, sepse rëndom prodhimi f g nuk ekziston, nuk ka kuptim.
- S h e m b u l l i 17. - Të caktohet shumëzimi i pasqyrimeve f :A→B dhe g :B→C , ku A {1, 2, 3, 4}, B {a, b, c, d} , nëse është :
f 
|
1 2 3 4
|
|
, g
|
a b c d
|
|
| b d a c e
|
α γ δ β
|
- Zgjidhje : Prodhimi g f:A→C është :
(g f)(1) g ( f(1) ) g(b) γ ,
(g f)(2) g ( f(2) ) g(c) δ ,
(g f)(3) g ( f(3) ) g(a) α ,
(g f)(4) g ( f(4) ) g(d) β ,
- pra :
| f g
|
a b c d
|
|
|
1 2 3 4
|
|
|
1 2 3 4
|
|
| α γ δ β
|
b d a c e
|
γ δ α β
|
- Këtu shumëzimi f g nuk është i përkufizuar .
- S h e m b u l l i 18. - Të caktohen shumëzimet
- (1) g f, (2) f g, (3) g-1 g ,
- ku f, g janë dy pasqyrime të dhëna me formulat :
f (x) x2 + 2x -1, g (x) 3x + 2 .
- Z g j i d h j e : :
- (1) (g f)(x)
|
g(f (x)) g(x2 + 2x-1) 3(x2+2x-1)+2
|
|
3x 2 +6x-1 ; |
|
- (2) (f g) (x)
|
f (g (x)) f (3x + 2) (3x + 2)2 + 2(3x + 2) -1
|
|
9x2 + 18x+7 ;
|
- (3) Meqë g -1 (x)
|
(x-2)
|
, (g-1 g)(x) g-1 (3x+2) x .
|
|
|
| 3
|
|
- Siç shihet pra, edhe kur ekzistojnë dy shumëzime g f dhe f g të funksioneve f, g vlera e tyre varet nga renditja e pasqyrimeve . Prandaj, konkludojmë se shumëzimi i pasqyrimeve f, g është veprim jokomutativ :
g f  f g ose g (f (x)) f (g (x)) . (...40)
|
