- P ë r k u f i z i m i 2.1.2. - Bashkësia e pjesëve të bashkësisë A quhet bashkësia e të gjitha nënbashkësive të bashkësisë A, pra :

Fig. 1.1.
|
P(A) {X {X X X A} . (...9) A} . (...9)
- Në bazë të këtij përkufizimi mund të konkludohet se bashkësia dhe elementi janë koncepte relative - A mund të konsiderohet si bashkësi të elementeve të caktuara A
 {x {x F(x)} , por edhe si element i bashkësisë së caktuar A F(x)} , por edhe si element i bashkësisë së caktuar A P(A) . P(A) .
- Nëse bashkësia A është e fundme [1] dhe ka n elemente, atëherë bashkësia P(A) ka
  2n elemente. 2n elemente.
- P ë r k u f i z i m i 2.1.3. - Dy bashkësi A, B janë të barabarta atëherë dhe vetëm atëherë, kur A
 B dhe B B dhe B A , pra : A , pra :
A B B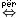 A A B B B B A. (...10) A. (...10)
- Për shembull: {a, b, c}
 {b, a, c}. {b, a, c}.
2.2. VEPRIMET ME BASHKËSI
- P ë r k u f i z i m i 2.2.1. - Prerja e bashkësive A. B quhet bashkësia e të gjitha e1ementeve të përbashkëta të bashkëswe A, B (fig. 1.2.), pra :

Fig. 1.2.
|
A B B {x {x x x A A x x B} . (...11) B} . (...11)
- Simboli
 (lexo: prerja ose itersekston) është shenja e veprimit të prerjes (interseksiont). (lexo: prerja ose itersekston) është shenja e veprimit të prerjes (interseksiont).
- P.sh. : {1,3,4,6}
 {2, 3, 5, 6, 8} {2, 3, 5, 6, 8} { 3, 6 } . { 3, 6 } .
- Në bazë të përkutizimit 2.2.1 . del se A
    për çfarëdo bashkësi A. Për çfarëdo dy bashkësi A, B kemi inkluzionet: për çfarëdo bashkësi A. Për çfarëdo dy bashkësi A, B kemi inkluzionet:
A B B A dhe A A dhe A B B B. B.
- Kur A
 B , atëherë A B , atëherë A B B A . Kur A A . Kur A B dhe A B dhe A C , atëherë A C , atëherë A B B C . C .
- Nëse A
 B B  , thuhet se bashkësitë A, B janë disjunkte. , thuhet se bashkësitë A, B janë disjunkte.
- ↑ 10)Bashkësitë të fundme dhe të pafundme përkufizohen në p. 4.1.
|






