Hipi Zhdripi i Matematikës/3
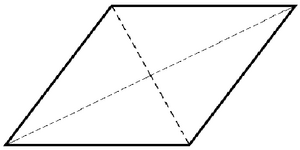 Fig.1: Përkufizimi gjeometrik i paralelogramit | |
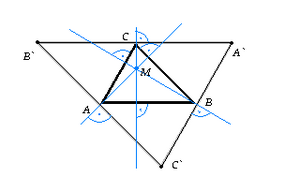 Fig. 2 : Vërtetimi i thënjes mbi qendren e trekëndshit | |
 Fig. 3 : Konstruktimi i katërkëndshit |
- Gjeometria e pasqyrimeve është një metod në gjeometri e cila provat dhe konstruktimet i krijon me ndihmen e elementeve të gjeometrisë.
- Me anë të elementeve gjeometrike tregohen vetit e pasqyrimeve si kongruenca, ngjashmëria (ekuivalenca), afinia etj. Po ashtu me këto elemente mund të vizatohen edhe përkufizimet e pasqyrimit.
- Për shembull përkufizimi me ndihmën e gjeometrisë do të ishte një katërkëndësh i cili pasqyrimin e pikave në vetvete quhet Paralelogram.
- Për shembull vërtetimi i një teorem me ndihmën e gjeometrisë.
- Me ndihmën e normaleve, duhet të vërtetohet se lartësitë e kulmeve të trekëndëshit ABC priten në një pikë.
- Të shikojmë trekëndëshin A', B', C', trekëndësh i ndërtuar mbi kulmet e trekëndëshit ABC (Shih Fig. 2). Të lëshojmë normalet nga kulmet A, B dhe C. Këto drejtëza do të priten sikurse priten në çdo trekëndësh në qendrën e trekëndëshit që ne e kemi paraqitë me M. Segmentet me një qendër M dhe me faktorin 1/2 të segmenteve formojnë trekëndëshin A'B'C' mbi trekëndëshin e brendshëm A,B,C. Ku, normalet në mesin e brinjëve të trekëndëshit A'B'C' i tejkalojnë lartësitë e trekëndëshit të brendshëm. Kështu lartësirat e trekëndëshit ABC priten në pikën M.
 |
 |

|
- Për shembull konstruktimi i figurave gjeometrike me ndihmën e pasqyrimit.
- Detyra është që përbrenda një trekëndëshi të konstruktohet një katror. Dy kënde të katrorit duhet që të prekin segmentin AB, ndërsa dy këndet tjera secili nga një në segmentet BC dhe AC
- Konstruktohet së pari një katrorë me dy kënde në AB dhe një këndë në AC. Pastaj nëpër gjurmët e një normale të lëshuar nga segmenti BC që kalon nëpër pikën A, tërhiqet katrori deri sa këndi i lirë i tij të prekë segmentin BC.
 |

|
< 2 |
faqe - 3 - |
4 > |