Hipi Zhdripi i Matematikës/2
Pasqyrimi NË ENCIKLOPEDI
- Pasqyrimi në matematikë është përkufizim themelorë, pa të cilin nuk do të kishte kuptim vetë lënda e matematikës. Matematika është pasqyrim i marrëveshjeve që njerëzit gjatë zhvillimit të tyre natyrorë kanë bërë ndërmjet veti. Në të vërtet matematika është një përmbledhje e marrëveshjeve që njerëzit kanë bërë ndërmjet veti nëpër gjenerata. Ajo nuk na paraqet marrëveshjet që janë shkelur por vetëm ato që njerëzit më të mençur të gjithë njerëzimit nëpër kohëra na kanë lënë si trashëgimi të cilën mund ta pasurojnë/korrigjojnë vetëm ata që kanë logjikë më të aftë se gjithë njerëzit para tij.
- Siç thamë pasqyrimi është përkufizim themelorë me të cilin rregullohet pasqyrimi i elementeve të një bashkësie në elementet e bashkësisë tjetër. Për pasqyrim përdoren edhe fjalë tjera që kanë të njëjtin funksion, po pra "funksioni" apo "relacioni". Mirëpo për të kuptuar e gjithë bota përdoren shprehjet matematikore. P.sh.:
- ,
- e cila në gjuhen shqipe lexohet “Bashkësia jo e zbrazët pasqyrohet në bashkësinë jo të zbrazët ” ose më shkurtë “ pasqyrohet në ”, edhe më shkurt “ në ”. Gjatë shkurtimeve sipas marrëveshjeve nënkuptohet se për se është fjala.
- Tani le të jetë një element i bashkësisë dhe element i bashkësisë dhe këtë po e shprehim si:
- dhe .
- Nëse ky pohim vlenë, atëherë për përgjithësim mund të shkruajmë shprehjet:
 Fig 1 Diagrami shigjetorë |
Shembull 1
- Secilit nxënës të një shkolle i është caktuar një klasë, të cilës do t´i takojë. Në fig.1 është bashkësia e nxënsve dhe bashkësia e klasëve. Këtu kemi një pasqyrim
:p.sh.: - I tërë pasqyrimi mund të pasqyrohet edhe i vizatuar. Për këtë zakonisht përdoren shigjetat që nga origjina (nxënsi) tregojnë përftyrimin (klasat)
Shembull 2
- Mësuesi i muzikës i jepë secilit nxënës notën.
|
- Edhe ky shembull është një pasqyrim. Paraqitjet e tilla të pasqyrimeve quhen paraqitje tabelare apo tabela e pasqyrimit.
Shembull 3
- Pasqyrimi parashehë që çdo numri të bashësisë së numrave natyral të i përgjegjet mbledhja e tërthort e shifrave të vetë numrit natyralë. d.m.th:
| P.sh.: | |
| sepse | |
| sepse | |
| sepse |
Shembull 4
- Pasqyrimi parashehë që çdo numri të bashësisë së numrave natyral të i përgjegjet katrori i vetë numrit natyralë, d.m.th prap:
| mirëpo: | |
| sepse | |
| sepse | |
| sepse |
- dhe kështu me radhë mund të pasqyrohen gjitha numrat. Për të përmgjithsuar rastin, d.m.th për të shprehur rastin sa më shkutë ashtu që mos ketë nevojë që gjithë të përsëritet kjo shprehje e gjatë disa e shprehin shkurt:
- apo duke paraqitë të dhënat e funksionit për të thuhet është japur funksioni i sistemit (shih: shprehja matematikore).
Shembull 5
- Çdo numër natyral n, më i vogël apo i barabart me 2, le të i pasqyrohet numri prim i pjesëve të vetë numrit natyral. Për të paraqitur më karrtë këtë rastë vizatohet një rrjetë e numrave si në figurën 2.
| Fig. 2 Paraqitja në rrjeten e numrave
|
Shembull 6
- Çdo numër real le të pasqyrohet në numrin e fituar nga shprehja . Pra, kemi një pasqyrim si më lartë pasqyrimin e elementeve të një bashkësi nga e cila krijohet një nën bashkësi.
-
me të dhënat:
- Në sistemin kordinatim karderzial mund të tregohet një figurë e cila paraqetë grafikun e këtij funksionit. Shih figurën 3.
Shembull 7
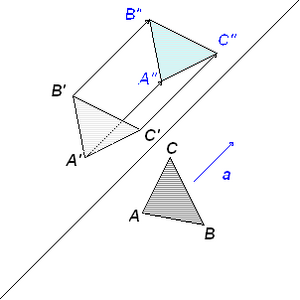 Fig. 4 : Kongruenca Fig. 4 : Kongruenca
|
- Në rrafshin e vizatimeve gjeometrike le të pasqyrohet çdo pikë e drejtëzës dhe me anë një vektori le të tërhiqet/shtyhet ai pasqyrim. Me këtë rastë do të fitojmë një pasqyrim kongruent të vetë rrafshit. Shih figurën 4.
Shembull 8
- Pasqyrimi paraqshehë që çdo pike () në sistemin kordinativ kardezian të i përgjegjet një pikë tjetër (), ashtu që :
-
- Pra, është :
- p.sh. me :
- ku, është bashkësia e numrave realë ndërsa bashkësia e gjitha çifteve të numrave natyral. Krahaso me prodhimin karderzial.
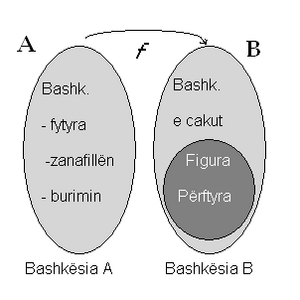
Rregullat e pasqyrimit
- Gjatë pasqyrimeve vlejnë disa rregulla. Bashkësin A e quajnë me terme që tregojnë bashkësin fillestare, zanafillën, burimin, domeni apo hapësirën e përufizuar, ndërsa për bashkësin B thuhet se është figura e A-së, caku, kodomeni. Bashkësia e elementeve të figurës quhen nën bashkësia e kodomenit, përftyrimi apo vlera e bashkësisë së përftyruar. Në përgithësi figura e elementeve të pasqyruara është një pjesë e bashkësisë koomene (të caktuar), si në shembullin 4, për cak ishte një pjesë e bashkësisë së numrave natyralë, d.m.th bashkësia e katrorëve të numrave natyral. Shih figurën 5.
- Pasqyrimi quhet NË, nga latinishtja : injektiv apo injukcion kur gjithnjë dy elemente të ndryshme të A-së pasqyrohen në dy elemente të ndryshme të B-së. Pra atëher kur për:
- , dhe vlenë , atëherë është
- Pasqyrimin injektiv në diagramet me shigjeta dallohen kur shigjeta niset nga një element i A-së dhe tregonë më së shumti një element të bashkësisë tjetër (B-së).
- Shembujt 4,7 dhe 8 janë pasqyrime injektive ndërsa paqyrimi në figurën e paraqtur më lartë nuk është injektiv.
- Pasqyrimi quhet surjektiv apo surjekcion kur çdo element i B-së është pasqyrim i elementeve të A-së. Pra bashkësia B dhe përftyra (vlera e caktuar) e pasqyrimit janë të barabarta.
- Pasqyrimi quhet MBI, bijektiv ose bijekcion kur është injektiv dhe surjektiv.
< 1 |
faqe - 2 - |
3 > |